
| 비교정렬 | 선택 정렬, 버블 정렬, 삽입 정렬, 퀵 정렬, 힙 정렬, 병합 정렬 등 |
| 비(非)비교정렬 | 계수 정렬, 기수 정렬, 버킷 정렬 |
| 안정 정렬(Stable sort) | 동일한 값에 대해 기존의 순서가 유지되는 정렬 방식 |
| 불안정 정렬(Not stable sort) | 동일한 값에 대해 기존의 순서가 뒤바뀔 수 있는 정렬 방식 |
| 제자리 정렬(In-place sort) | 주어진 공간 외에 추가적인 공간을 사용하지 않는 정렬 |
기본 정렬
(1) Selection Sort

단위 순환
- 최대 원소를 찾는다.
- 최대 원소와 맨 오른쪽 원소의 자리를 바꾼다.
- 맨 오른쪽 자리를 관심 대상에서 제외한다.
- 원소가 1개 남을 때까지 위의 순환을 반복한다.
비교 작업의 총 수가 수행 시간을 좌우한다.
| Worst | $$ O(n^2) $$ |
| Average | $$ O(n^2) $$ |
| Best | $$ O(n^2) $$ |
(2) Bubble Sort

단위 순환
- 맨 앞부터 한 칸씩 이동하면서, 두 원소가 순서대로 되어 있지 않으면 자리를 바꾼다.
- 맨 오른쪽 자리를 관심 대상에서 제외한다.
- 원소가 1개 남을 때까지 위의 순환을 반복한다.
비교 작업의 총 수가 수행 시간을 좌우한다.
| Worst | $$ O(n^2) $$ |
| Average | $$ O(n^2) $$ |
| Best | $$ O(n^2) $$ |
(3) Insertion Sort
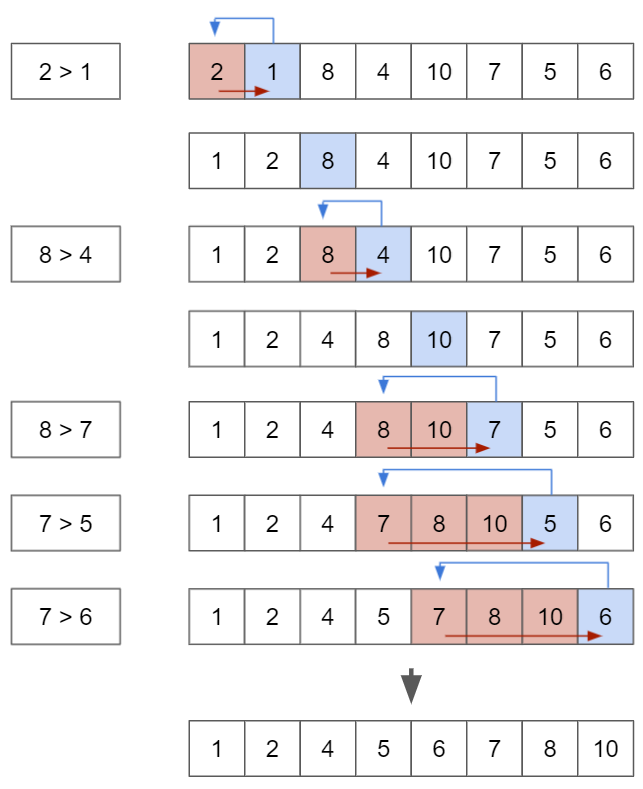
- 삽입 정렬은 특정한 데이터가 적절한 위치에 들어가기 이전에 그 앞까지의 데이터는 이미 정렬되어 있다고 가정한다.
- 정렬되어 있는 데이터 리스트에서 적절한 위치를 찾은 뒤에, 그 위치에 삽입된다.
- 구현 난이도가 높은 편이지만, 선택 정렬에 비해 복잡도 측면에서 더 효율적인 알고리즘이다.
삽입에 소요되는 비교 횟수, shift 횟수가 수행 시간을 좌우한다.
| Worst | $$ O(n^2) $$ |
| Average | $$ O(n^2) $$ |
| Best | $$ O(n) $$ |
고급 정렬
(1) Merge Sort

- 병합 정렬은 정렬되지 않은 전체 데이터를 분할한 후에, 정렬한다.
- 정렬된 데이터들을 다시 병합해나가는 알고리즘이다.
- 항상 O(nlogn) 시간이 소요된다.
| Worst | $$ O(nlogn) $$ |
| Average | $$ O(nlogn) $$ |
| Best | $$ O(nlogn) $$ |
(2) Quick Sort

단위 순환
- 하나의 기준(pivot)을 정한다.
- 이 기준보다 작은 값은 왼쪽, 큰 값은 오른쪽에 위치시킨다.
- 원소가 1개 남을 때 까지 위의 순환을 반복한다.
- 이름에서 알 수 있듯이 평균적으로 매우 빠르다. 그러나, 같은 원소가 많아지면 그만큼 성능이 떨어진다.
- 모든 원소가 동일하면 선택 정렬 수준으로 떨어진다.
- 같은 원소의 그룹들이 있으면 그룹들의 크기가 클수록 성능이 떨어진다.
| Worst | $$ O(n^2) $$ |
| Average | $$ O(nlogn) $$ |
| Best | $$ O(nlogn) $$ |
특수 정렬
(1) Counting Sort
계수 정렬은 특정한 조건이 부합할 때만 사용할 수 있지만, 매우 빠르게 동작하는 정렬 알고리즘이다.
- 특정한 조건이란 계수 정렬은 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용이 가능하다는 것이다.
- 일반적으로 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000을 넘지 않을 때 효과적으로 사용할 수 있다.
- 계수 정렬은 동일한 값을 가지는 데이터가 여러개 등장할 때 효과적으로 사용할 수 있다.
- (Ex) 학생들의 성적, 자동차들의 속도 데이터
| Worst | $$ O(n+k) $$ |
| Average | $$ O(n) $$ |
| Best | $$ O(n) $$ |
(2) Radix Sort
기수 정렬은 계수 정렬과 마찬가지로 비교 연산을 수행하지 않아 조건이 맞는 상황에서 빠른 정렬 속도를 보장하는 알고리즘이다.
- 데이터의 각 자릿수를 낮은 자리 수에서부터 가장 큰 자리 수까지 올라가면서 정렬을 수행하는 것이다.
- 그렇기에, 자릿수가 존재하지 않는 데이터를 기수 정렬로 정렬하는 것은 불가능하다.
| Worst | $$ O(nk) $$ |
| Average | $$ O(nk) $$ |
| Best | $$ O(n) $$ |
예시)
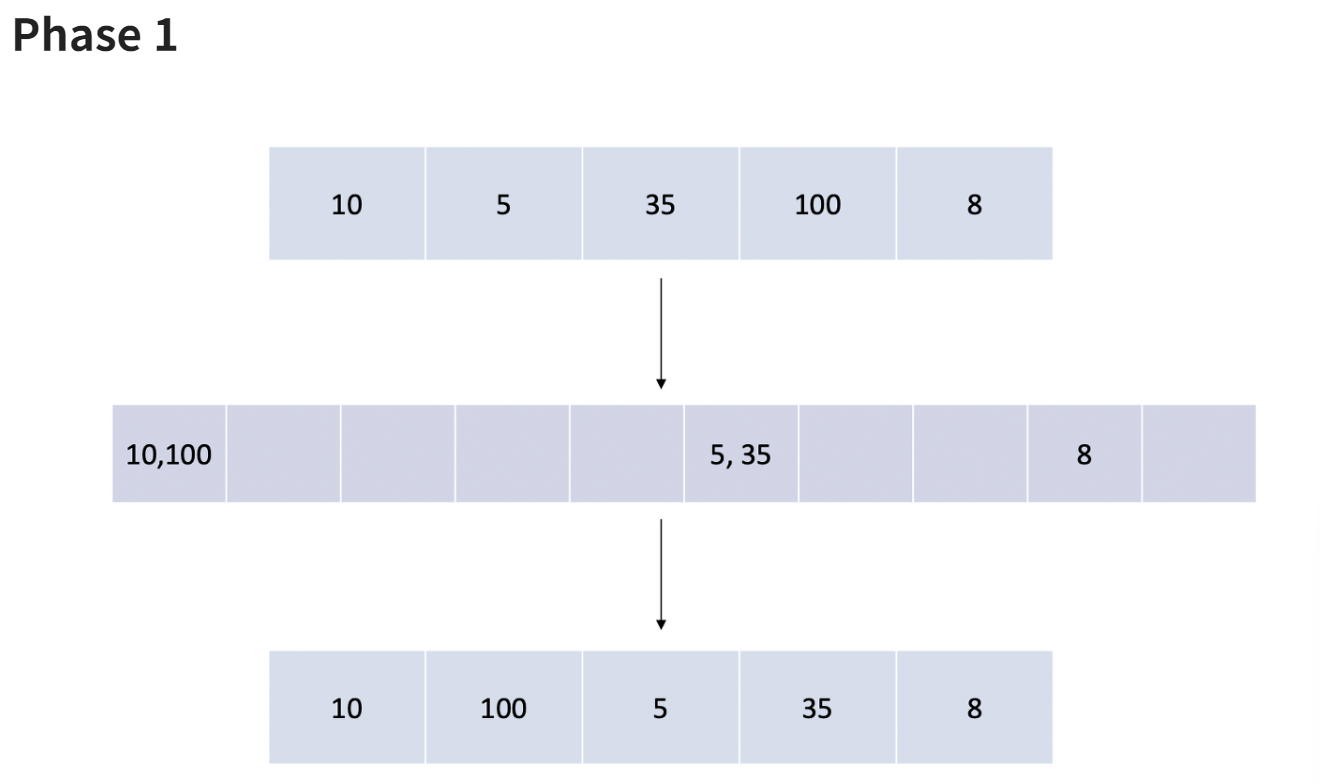
- 각 데이터들을 1의 자리끼리 비교해서 정렬한다.
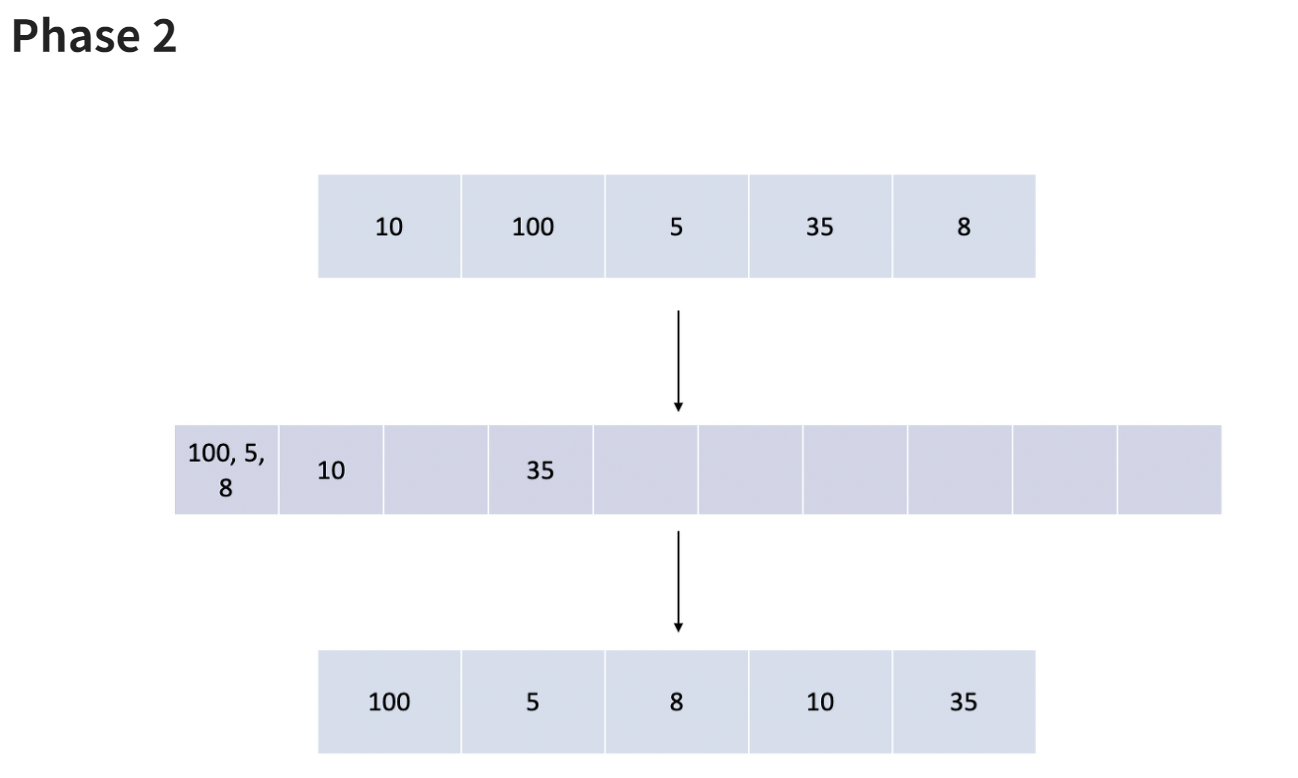
- 1의 자리까지 정렬된 배열을 다시 10의 자리를 기준으로 정렬한다.
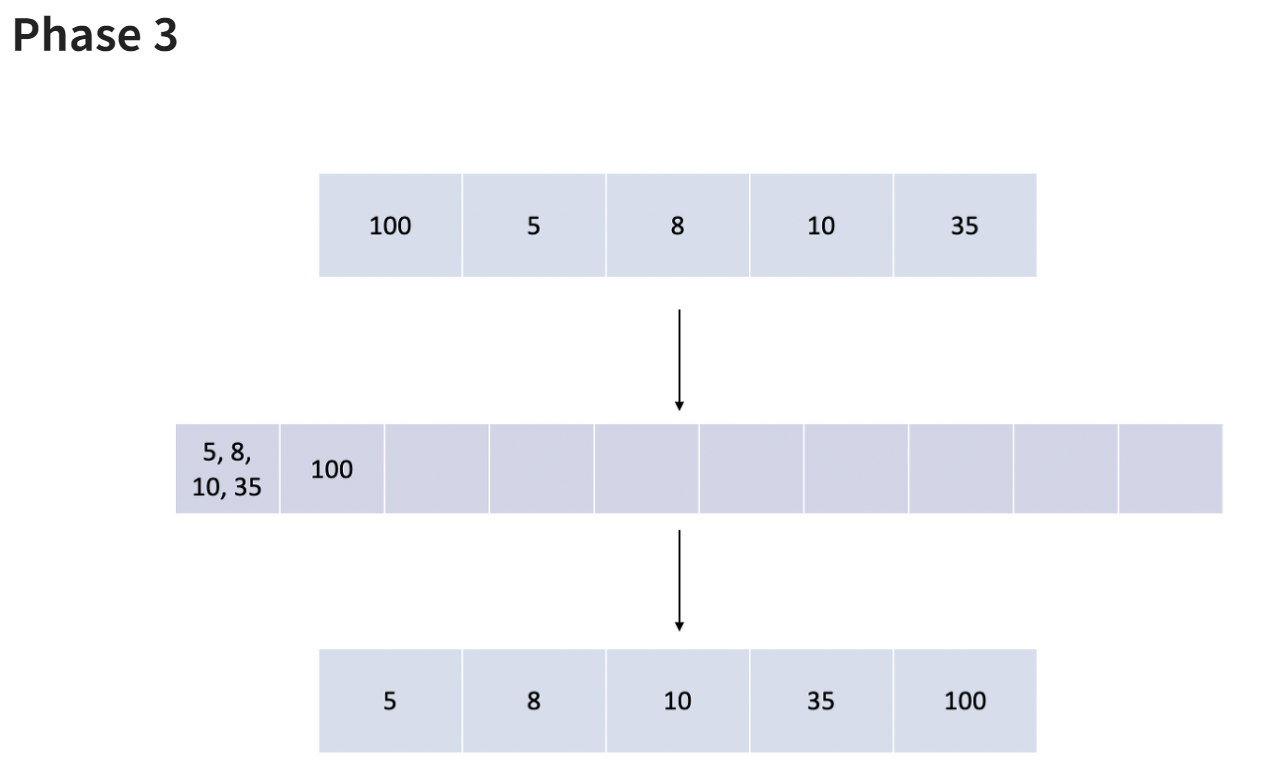
- 마지막으로 100의 자리를 기준으로 정렬한다.
(3) Bucket Sort
버킷 정렬은 계수 정렬을 일반화한 것으로 간주할 수 있다.
- 계수 정렬은 키값이 작은 범위 안에 들어올 때 적용할 수 있는 방법이지만 버킷 정렬은 키값의 범위 뿐만 아니라 그 범위 내에서 키값이 확률적으로 균등하게 분포된다고 가정할 수 있을 때 적용할 수 있는 방법이다.
| Worst | $$ O(n^2) $$ |
| Average | $$ O(n+k) $$ |
| Best | $$ O(n) $$ |
예시)

- 데이터 n개가 주어졌을 때, 데이터의 범위를 n개로 나누고 이에 해당하는 n개의 버킷을 만든다.
- 각각의 데이터를 해당하는 버킷에 넣는다.
- 같은 버킷 안의 들어가는 원소들은 다시 리스트로 보관한다.
- 버킷 별로 리스트 안에 들어있는 원소들의 정렬을 진행한다.
- 버킷 간에는 정렬이 되어 있으므로 이를 전체적으로 합치면 전체가 정렬된다.
'Coding Test > Sorting' 카테고리의 다른 글
| [Sorting] H-Index (2) | 2024.06.13 |
|---|---|
| [Sorting] 가장 큰 수 (0) | 2024.06.13 |
| [Sorting] K번째 수 (0) | 2024.06.13 |